表1 玻璃纤维聚合物筋混凝土梁抗弯强度的试验结果

---

CB4B-1 230.10 1.515 45 10.00 0.828 75.4 67.638 0.158 受压 CB4B-2 230.10 1.515 45 14.00 1.160 71.7 67.638 0.151 受压 CB6B-1 230.10 2.272 45 10.00 0.828 84.8 78.210 0.178 受压 CB6B-2 230.10 2.272 45 14.00 1.160 85.4 78.210 0.179 受压 ST2B 229.10 2.559 46 23.00 1.884 110.4 111.810   受拉

---

注：ST、KD和CB分别代表Isorod筋、Kodiak筋和C-bar筋混凝土梁 www.tmgc8.com

1.1 配筋率对抗裂弯矩的影响　引入系数α_cr反映配筋率对开裂弯矩的影响，α_cr定义为：

α_cr=6Ｍ_cr·exp /bh²f_r

(1)

式中：α_cr是一系数；M_cr·exp是由试验得到的开裂弯矩承载力或抗裂弯矩承载力；b和h分别是梁的宽度和高度；fr是混凝土的拉伸强度，计算式为fr=0.6f′c.

　　利用式(1)基本上消除了尺寸效应和混凝土强度的影响。各梁的α_cr值可以根据表1中的试验数据计算得到。图1分别是Kodiak和Isorod纤维聚合物筋混凝土梁α_cr的平均值与配筋率的关系图。从图中可以明显地看出，配筋率对开裂弯矩的影响非常有限，不同类型筋的α_cr值基本相同，并近似地等于1.这是因为当开裂弯矩达到时，纵筋的应力非常小，抗裂弯矩主要取决于混凝土的抗拉强度。

1.2 配筋率对抗弯承载力的影响　配筋率对适筋梁极限承载力的影响是很明显的，这里主要讨论配筋率对纤维聚合物超筋混凝土梁极限弯曲承载力的影响。与抗裂承载力的分析类似，为了减

图1 配筋率对玻璃纤维聚合物筋混凝土梁α_cr的影响

少截面尺寸和混凝土强度的影响，引入另一个系数α_u，其定义为：

αu=M_u·exp/bd²f′_c

(2)

式中：α_u是一系数；M_u·exp是由试验得到的极限弯矩承载力；d是梁的有效高度。

　　根据试验结果由式(2)计算得到剪压破坏各梁的α_u值，见表1.Kodiak和Isorod纤维聚合物筋混凝土梁α_u的平均值与其对应的配筋率的关系见图2.可以看出，当配筋率超过一定值时，α_u或弯矩M_u随着配筋率的增加而增大。这是因为对于相同尺寸的梁，纤维聚合物筋越多，受压区面积越大，极限弯曲承载力越高；然而，当纤维聚合物筋的增多使受压区面积增大到一定程度时，内力臂将减小，使极限弯曲承载力的增加与配筋率的增大不成比例，并且还可能受到剪切破坏的限制。

2 开裂弯矩

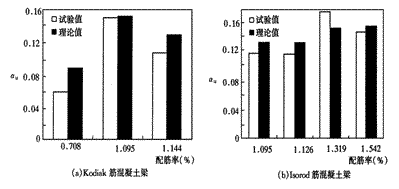
图2 配筋率对纤维聚合物筋混凝土梁α_u的影响

　　由表1、图1的试验结果可知，尽管玻璃纤维聚合物筋和钢筋属于不同类型的增强材料，但它们对钢筋混凝土梁和玻璃纤维聚合物筋混凝土梁开裂弯矩或抗裂弯矩的影响程度基本相同。

　　根据本文的试验数据，Isorod、Kodiak、C-bar和钢筋混凝土梁α_cr的平均值分别是0.961、0.988、1.034和1.188.4种增强材料的α_cr的平均值是1.043.这表明用ACI318-M96规范中采用的式(3)计算纤维聚合物筋混凝土梁的开裂弯矩是比较合适的。

www.tmgc8.com

M_cr=f_rI_g/y_t

(3)

式中：M_cr是开裂弯矩或抗裂弯矩；y_t是受拉边缘到中性轴的距离；I_g是未开裂截面的惯性矩。

　　例如，对玻璃纤维聚合物单筋矩形截面混凝土梁，未开裂截面的惯性矩为：

Ig=1 12bh3［1+1.7(n-1)ρ

(4)

式中：ρ是纵筋的配筋率，ρ＝A_f/(bd)；n是玻璃纤维聚合物筋弹性模量与混凝土弹性模量的比值。

3 弯矩曲率关系　　图3(a)所示的玻璃纤维聚合物单筋混凝土梁截面的弯矩曲率关系可以通过一般的弯曲理论得到。由于混凝土抗拉强度低，截面开裂后拉应力主要由玻璃纤维聚合物筋承担。因此，若忽略受拉区混凝土的作用，受压区混凝土应力由混凝土的应力-应变关系得到，那么玻璃纤维聚合物单筋混凝土梁截面的弯矩曲率关系可以由以下方程联合求出。

上一页  [1] [2] [3] [4] [5]  下一页

上一篇：谈桥梁工程施工安全的具体措施