纤维塑料筋混凝土梁设计理论研究
[12-11 16:59:19] 来源:http://www.tmgc8.com 工程设计 阅读:3945次
纤维塑料筋(Fiber Reinforced Polymer/Plastic Rebars,简称FRP筋)具有轻质、高强、耐腐蚀和抗疲劳等优点,是混凝土结构中钢筋或预应力钢筋的理想替代材料[1]。国外对FRP筋混凝土结构的研究起步较早,日本、加拿大、美国已相继颁布了关于FRP筋混凝土结构的设计规范。在国内,本课题组于1995年率先开展了FRP筋混凝土结构的研究工作[2]。目前,本课题组己完成了一系列关于FRP筋混凝土梁的试验研究与理论分析,主要包括:CFRP筋、GFRP筋的粘结性能研究[3~7];非预应力FRP筋混凝土梁单调静力性能研究[8,9];有粘结、部分粘结预应力CFRP筋混凝土梁单调静力性能研究[10~15];有粘结、部分粘结预应力CFRP筋混凝土梁在低周反复荷载作用下的受力性能研究;预应力CFRP筋混凝土梁在300万次疲劳荷载作用下的受力性能研究[16~18],等等。
本文简要介绍本课题组近年来关于FRP筋混凝土梁设计理论的研究工作,主要包括FRP筋粘结性能设计建议、非预应力FRP筋混凝土梁设计理论、有粘结与部分粘结预应力FRP筋混凝土梁设计理论。此外,还初步提出了预应力CFRP筋混凝土梁疲劳性能与抗震性能的设计建议。
1 FRP筋粘结性能设计建议
1.1 CFRP筋粘结性能设计建议
通过48个拉拔试件对高性能CFRP绞线筋与不同环境介质之间的粘结性能进行了研究[4,5]。试件设计参数为:①环境介质(包括普通混凝土C50、掺聚丙烯纤维和磨细矿渣的高性能混凝土C50、环氧树脂及R42.5水泥浆);②配筋种类(分为CFRP绞线筋和钢绞线);③CFRP筋直径(分为φFRP15.2mm和φFRP12.5mm)。基于粘结试验研究,提出了CFRP绞线筋的锚固长度计算公式与粘结应力一滑移曲线理论方程。
1.1.1 锚固长度
高性能CFRP绞线筋的锚固长度ιbf可按下式进行计算[5]:
![]()
式中:ffu(MPa)为CFRP绞线筋的极限抗拉强度;db(mm)为CFRP绞线筋直径;f’c(MPa)为混凝土圆柱体抗压强度;K为与环境介质相关的常数(对于混凝土、水泥浆和环氧树脂,K分别取为0.083,0.167和0.056)。
1.1.2 粘结应力-滑移拟合曲线
采用CurveExpert软件对拉拔试件的粘结应力-滑移曲线(即τ-S曲线)进行了拟合。典型试件的τ-S拟合曲线如图1所示。
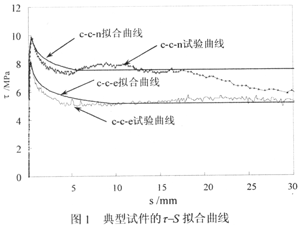
1.2 粘砂变形GFRP筋粘结性能设计建议
共设计了18个梁式试件和48个拉拔试件[6,7],试件设计参数包括:①筋的种类(GFRP筋和变形钢筋);②试件形式(梁式试件、Losberg拉拔试件和标准拉拔试件);③筋直径db(6mm~19mm);④粘结长度(2.5db~20db)。基于粘砂变形GFRP筋梁式试验与拉拔试验,综合考虑GFRP筋直径、表面形态和粘结长度等因素,提出了GFRP筋锚固长度的设计建议,并对其粘结滑移本构关系进行了研究。
1.2.1 锚固长度
GFRP筋锚固长度ιa按下式进行计算[6]:
![]()
式中:λ≥1,为安全系数;fu(MPa)为GFRP筋的极限抗拉强度;τu(MPa)为粘结强度;ft(MPa)为混凝土的轴心抗拉强度;α’为GFRP筋表面形态影响系数(对于粘砂变形GFRP筋,α’=1.0;对于“绕肋粘砂”、“粘砂”和“织物”类GFRP筋,α’可分别取0.64、0.39和0.67)。需要说明,式(2)适用于混凝土fc<50MPa的情况。
1.2.2 粘结滑移本构关系
试验研究表明,GFRP筋试件的粘结应力—滑移曲线(τ-S曲线)可分为微滑移段、滑移段、下降段和残余段,区分这四段的三个特征点分别为弹性滑移点、峰值滑移点和残余滑移点。基于试验结果,提出了粘砂变形GFRP筋与混凝土之间粘结滑移本构关系的理论模型www.tmgc8.com[7](如图2)。

2 非预应力FRP筋混凝土梁设计理论
本课题组先后开展了9根FRP筋混凝土梁的单调静力试验研究,并进行了38根FRP筋混凝土梁的非线性有限元参数分析。基于本课题组及国外相关研究成果,对FRP筋混凝土梁的正截面抗弯承载力、裂缝宽度、挠度计算方法等进行了较为系统的研究[8,9]。
FRP筋混凝土梁的破坏模式分为受拉破坏、平衡破坏和受压破坏三种。FRP筋混凝土梁正截面抗弯承载力可按式(3)进行计算[8]:

上式中:Af(mm2)为FRP筋面积;ffy(MPa)为FRP筋名义屈服强度;ffu(MPa)为FRP筋的极限抗拉强度;pf,pmin和Pfb分别为实际配筋率、最小配筋率和平衡配筋率。其他符号意义参见我国现行《混凝土结构设计规范》。
采用上述抗弯承载力建议公式计算了国内外149根FRP筋混凝土梁的正截面抗弯承载力,对比表明,该建议公式的计算值与试验值和参数分析结果吻合良好。
3 有粘结预应力FRP筋混凝土梁设计理论
本课题组先后进行了6根有粘结预应力CFRP筋混凝土矩形梁、两根有粘结预应力CFRP筋混凝土T型梁以及两根体内外混合配置预应力CFRP筋混凝土T型梁的单调静力试验[10,11],并基于ANSYS软件进行了非线性有限元参数分析。基于本课题组与国外相关研究成果,对有粘结预应力FRP混凝土梁的正截面抗弯承载力、裂缝宽度及挠度计算方法等进行了较系统的研究[12~14]。
试验研究表明,有粘结预应力FRP筋混凝土梁的破坏模式包括界限破坏、受压破坏与受拉破坏三种。基于受弯截面的极限状态分析,推导出截面受拉区同时配置预应力FRP筋和非预应力钢筋(配筋形式一)、预应力FRP筋和非预应力FRP筋(配筋形式二)这两种混合配筋形式下的有粘结预应力FRP筋混凝土梁的正截面抗弯承载力计算公式[12]。
对于配筋形式一的混凝土梁,其正截面抗弯承载力可按如下公式进行计算:
(1)界限破坏
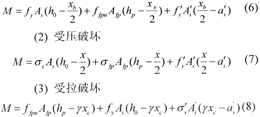
上式中:Afp(mm2)和ffpu(MPa)分别为预应力FRP筋的面积和抗拉强度值;γ为受拉破坏时混凝土受压区边缘至压应力合力作用点的距离与实际受压区高度Xc之比。其他符号意义参见我国现行《混凝土结构设计规范》。
对于配筋形式二的有粘结预应力FRP筋混凝土梁,其抗弯承载力计算公式也可由截面的平衡状态分析得到。需指出,此时根据FRP筋的断裂次序可考虑两种不同受拉破坏形式:预应力FRP筋先于非预应力FRP筋拉断和非预应力FRP筋先于预应力FRP筋拉断。
应用该建议公式对本课题组以及国外完成的48根有粘结预应力FRP筋混凝土梁的试验结果和6根梁的参数分析结果进行了计算与对比,对比表明,计算值与试验结果和参数分析结果吻合较好。
4 部分粘结预应力FRP筋混凝土梁设计理论
通过9根梁的单调静力全过程试验与非线性有限元参数分析,对部分粘结预应力CFRP筋混凝土梁的受力过程、破坏形态、抗弯承载力、变形能力和延性性能等进行了较为系统的研究。综合考虑无粘结段长度比例、外荷载形式、综合配筋指数、预应力筋布置方式等因素,以无粘结段预应力FRP筋与相应处混凝土变形协调条件为
依据,根据弹性力学原理推导了预应力FRP筋的弹性应力增量,提出了采用迭代法求解预应力FRP筋的极限应力增量计算方法,并在此基础上提出了部分粘结预应力FRP筋混凝土梁预应力损失、抗裂度、抗弯承载力、挠度和裂缝宽度等的设计建议。
部分粘结预应力FRP筋混凝土梁的正截面抗弯承载力计算可按下式进行[15]:
 www.tmgc8.com
www.tmgc8.com
上式中,σpu(MPa)为无粘结段预应力筋的极限应力;其他符号意义同上或参见我国现行《混凝土结构设计规范》。
5 预应力CFRP筋混凝土梁疲劳性能设计建议
以某实际工程桥梁为原型设计了3根部分预应力CFRP筋混凝土梁试件(包括1根体内外混合配置预应力CFRP筋混凝土梁和两根体内预应力CFRP筋混凝土梁)和1根体内体外混合配置预应力筋的钢筋混凝土梁对比试件
